一文详解二叉树

Posted on | In

树是一种重要的数据结构，它的定义：

树(Tree)是n(n≥0)个结点的有限集。n=0时称为空树。在任意一颗非空树中：（1）有且仅有一个特定的称为 根（root） 的结点（2）当n>1时，其余结点可以分为m(m>0)个互不相交的有限集T1,T1,…,Tm，其中每一个本身又是一棵树，并且称为根的 子树（sub tree）

树的术语

  • 结点的度：结点拥有的子树个数。
  • 树的度：树内各结点的度的最大值。
  • 叶结点或终端结点：度为0的结点。
  • 子结点，父结点：结点的子树的根称为该结点的子结点，对应的，该结点是子结点的父结点。
  • 根结点：没有父结点的是根结点。
  • 结点的层次：根结点是第一层，根的子结点是第二层，依此类推。
  • 树的深度或高度：树中结点最大的层次称为树的深度或高度。

二叉树定义

二叉树（Binary Tree）是n（n≥0）个结点的有限集合，该集合或者为空集（空二叉树），或者由一个根结点和两棵互不相交的，分别称为根结点的左子树右子树的二叉树组成。

简单点说，树中所有结点的度不超过2，这样的树就是二叉树。

二叉树特点

  • 每个结点最多有两棵树。
  • 左子树和右子树是有顺序的，不能颠倒。
  • 即使树中某结点只有一个子树，也要区分是左子树还是右子树。

特殊二叉树

  • 斜树：所有结点都只有左子树的二叉树叫做左斜树，所有结点都只有右子树的二叉树叫做右斜树，这两者统称为斜树。

  • 满二叉树：所有分支结点都存在左子树和右子树，并且所有叶子结点都在最下面一层，这样的称为满二叉树。（满二叉树的结点个数为2^ｎ-1，ｎ为数的深度)。
    ）

  • 完全二叉树：若二叉树中最多只有最下面两层的结点的度数可以小于2，并且最下面一层的叶子结点都是依次排列在该层最左边的位置上，则称为完全二叉树。

二叉树的存储结构

顺序存储

当二叉树是完全二叉树时，我们可以使用顺序存储来存储二叉树，如下图所示：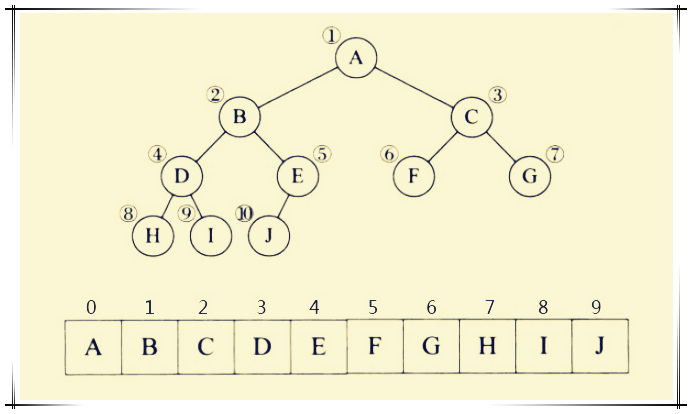
images
按层序遍历（下面会介绍）依次把结点存储在一个数组中。

对于非完全二叉树，也可以按顺序存储，但是相比完全二叉树缺少的结点用 ^ 代替，这样空间利用率不高，一般非完全二叉树不建议用顺序存储。

链式存储

二叉树每个结点最多只有两个孩子结点，所以为它设计一个数据域和两个指针域是比较好的做法，我们称这样的链表叫做二叉链表。结点的结构如下图所示：
images

下面是我们二叉链表结构定义代码：

1
2
3
4
5
static class Node<E> {
        E item;
        Node<E> leftChild;
        Node<E> rightChild;
    }

利用指针域我们便可以完美的存储非完全二叉树，如下：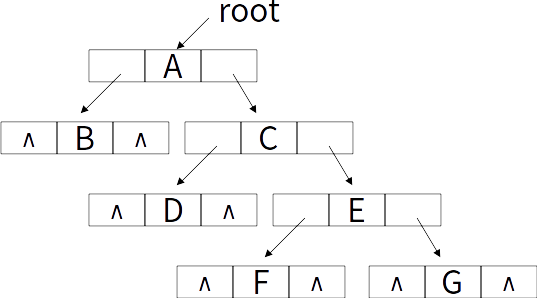
images

如果有需要，我们还可以增加一个指向父结点的指针域，那样就称之为三叉链表。

二叉树遍历

前序遍历

若二叉树为空，则直接返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。

递归算法实现：

1
2
3
4
5
6
7
8
public void firstOrderTraversal(Node<E> node) {
      if (node == null) {
          return;
      }
      printNode(node);
      firstOrderTraversal(node.leftChild);
      firstOrderTraversal(node.rightChild);
  }

非递归算法实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public void firstOrderTraversal2(Node<E> node) {
      if (node == null) {
          return;
      }
      Stack<Node<E>> stack = new Stack<>();
      stack.push(node);

      while (!stack.isEmpty()) {
          Node<E> pop = stack.pop();
          if (pop != null) {
              printNode(pop);
              stack.push(pop.rightChild);
              stack.push(pop.leftChild);
          }
      }
  }

中序遍历

若二叉树为空，则直接返回，否则先从根结点开始（注意不是先从根结点访问），中序遍历根结点的左子树，然后访问根结点，最后中序遍历根结点的右子树。

算法实现：

1
2
3
4
5
6
7
8
9
public void inOrderTraversal(Node<E> node) {
        if (node == null) {
            return;
        }
        inOrderTraversal(node.leftChild);
        printNode(node);
        inOrderTraversal(node.rightChild);

    }

非递归算法实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public void inOrderTraversal2(Node<E> node) {
    if (node == null) {
        return;
    }
    Stack<Node<E>> stack = new Stack<>();

    while (node != null || !stack.isEmpty()) {
        if (node != null) {
            stack.push(node);
            node = node.leftChild;
        } else {
            Node<E> pop = stack.pop();
            printNode(pop);
            node = pop.rightChild;
        }
    }
}

后序遍历

若二叉树为空，则直接返回，否则先从根结点开始，后序遍历根结点的左子树，然后中序遍历根结点的右子树，最后访问根结点。

算法实现：

1
2
3
4
5
6
7
8
public void postOrderTraversal(Node<E> node) {
        if (node == null) {
            return;
        }
        postOrderTraversal(node.leftChild);
        postOrderTraversal(node.rightChild);
        printNode(node);
    }

非递归算法实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * 主要思想：首先遍历root根节点的所有左结点，并依次入栈。对出栈的元素，如果没有右子树或者虽然有右子树
 * 但右子树已完成遍历，即可完成出栈；否则，再次入栈，并把右子树入栈，遍历右子树的所有左子树。
 *
 * @param node
 */
public void postOrderTraversal2(Node<E> node) {
    if (node == null) {
        return;
    }
    Stack<Node<E>> stack = new Stack<>();
    Node<E> prePop = null;
    while (node != null || !stack.isEmpty()) {
        if (node != null) {
            stack.push(node);
            node = node.leftChild;
        } else {
            Node<E> pop = stack.pop();
            if (pop.rightChild == null || pop.rightChild == prePop) {
                printNode(pop);
                prePop = pop;
                node = null;
            } else {
                stack.push(pop);
                stack.push(pop.rightChild);
                node = pop.rightChild.leftChild;
            }
        }
    }
}

层序遍历

若二叉树为空，则直接返回，否则先从树的第一层，也就是根结点开始，从上而下逐层遍历，同一层中，按从左至右依次访问各个结点。

算法实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public void levelOrderTraversal(Node<E> node) {
        if (node == null) {
            return;
        }
        LinkedList<Node<E>> queue = new LinkedList<>();
        queue.push(node);
        while (!queue.isEmpty()) {
            Node<E> pop = queue.poll();
            if (pop != null) {
                printNode(pop);
                queue.add(pop.leftChild);
                queue.add(pop.rightChild);
            }
        }
    }